Caros Leitores;
Números de Dedekind
Depois de 32 anos de busca, matemáticos encontraram o 9º membro de uma das séries matemáticas mais desafiadoras que existem.
Embora você já deva estar a acostumado às comemorações envolvendo o cálculo de dígitos adicionais do número pi (π) ou dos maiores números primos, o cálculo do chamado "número de Dedekind" é ainda mais desafiador.
Os cinco primeiros números da série, de D(0) a D(4), foram identificados pelo próprio matemático Richard Dedekind [1831-1916] quando definiu o problema, em 1897. O D(5) foi calculado por Randolph Church em 1940 e o D(6) em 1946 por Morgan Ward.
A partir daí, foi necessário esperar a invenção dos computadores, com o D(7) sendo encontrado também por Church em 1965. Esperou-se então até a criação dos supercomputadores, com o D(8) sendo calculado em 1991 por Doug Wiedemann.
Agora, Lennart Van Hirtum e colegas das universidades Paderborn (Alemanha) e Lovaina (Bélgica) acabam de calcular o D(9), um gigantesco número com 42 dígitos: Exatamente 286386577668298411128469151667598498812366.
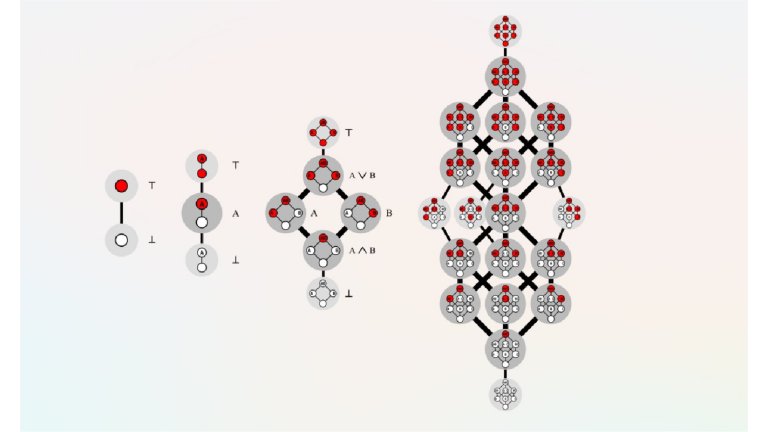
A figura mostra todos os cortes possíveis para as dimensões 0, 1, 2 e 3. O número desses cortes coloridos n-dimensionais que podem ser formados é definido como o número de Dedekind.
[Imagem: Lennart Van Hirtum]
O que é número de Dedekind?
Os números de Dedekind envolvem as chamadas funções booleanas monótonas.
"Basicamente, você pode pensar em uma função booleana monótona em duas, três e infinitas dimensões como um jogo com um cubo n-dimensional. Você equilibra o cubo em um canto e depois colore cada um dos cantos restantes de branco ou vermelho. Existe apenas uma regra: Você nunca deve colocar um canto branco sobre um vermelho.
"Isso cria uma espécie de interseção vertical vermelho-branco. O objetivo do jogo é contar quantos cortes diferentes existem. É este número de cortes que é definido como o número de Dedekind. Mesmo que não pareça, os números rapidamente se tornam gigantescos no processo: o 8º número de Dedekind já tem 23 dígitos," explicou Van Hirtum.
Embora os números de Dedekind sejam pouco conhecidos do público, números comparativamente grandes - mas incomparavelmente mais fáceis de calcular - são conhecidos por uma lenda sobre a invenção do jogo de xadrez.
"Segundo esta lenda, o inventor do jogo de xadrez pediu ao rei apenas alguns grãos de arroz em cada casa do tabuleiro de xadrez como recompensa: Um grão na primeira casa, dois grãos na segunda, quatro na terceira e o dobro em cada uma das casas seguintes. O rei rapidamente percebeu que este pedido era impossível de ser atendido, porque não existe tanto arroz em todo o mundo.
"O número de grãos de arroz no tabuleiro completo teria 20 dígitos - uma quantidade inimaginável, mas ainda menor que o D(8). Quando você percebe essas ordens de magnitude, é óbvio que tanto um método computacional eficiente quanto um computador muito rápido seriam necessários para encontrar o D(9)," disse Van Hirtum.
Tantos cálculos quantos grãos de areia na Terra
Por sorte, os matemáticos conseguiram as duas coisas, a começar pelo trabalho anterior do professor Patrick De Causmaecker, que se tornou um dos proponentes do projeto para o cálculo do D(9).
Causmaecker havia desenvolvido uma técnica conhecida como fórmula do coeficiente P. Essa fórmula fornece uma maneira de calcular os números de Dedekind não por contagem, mas por uma soma muito grande. Isso permite que D(8) seja decodificado em apenas oito minutos em um laptop normal. Contudo, o que leva oito minutos para D(8) chega a centenas de milhares de anos para o D(9).
O principal problema é que o número de termos nessa fórmula cresce incrivelmente rápido. "No nosso caso, explorando simetrias na fórmula, conseguimos reduzir o número de termos para 'apenas' 5,5 . 1018, uma quantidade enorme. Em comparação, o número de grãos de areia na Terra é de cerca de 7,5 . 1018, o que não é nada desprezível, mas para um supercomputador moderno, 5,5 . 1018 operações são bastante gerenciáveis," disse Van Hirtum.
Mas havia um problema: O cálculo desses termos em processadores normais ou mesmo em GPUs é lento, já que as tecnologias de aceleradores de hardware mais rápidas não são eficientes para esse algoritmo. A equipe então partiu em busca de um hardware específico de unidades aritméticas altamente especializadas e paralelas - as chamadas FPGAs (Matrizes de Portas Programáveis em Campo).
Van Hirtum desenvolveu um protótipo inicial para o acelerador de hardware e começou a procurar um supercomputador que tivesse as placas FPGA necessárias. Foi quando ele encontrou o supercomputador Noctua 2, da Universidade de Paderborn, que possui um dos sistemas FPGA mais poderosos do mundo.
O cálculo do D(9) exigiu cinco meses de trabalho desse supercomputador especial.
Para saber mais, acesse o link abaixo>
Fonte: Redação do Site Inovação Tecnológica - 28/06/2023
https://www.inovacaotecnologica.com.br/noticias/noticia.php?artigo=numero-dedekind&id=010150230628
=========================
Obrigado pela sua visita e volte sempre!
Web Science Academy; Hélio R.M.Cabral (Economista, Escritor e Divulgador de conteúdos de Economia, Astronomia, Astrofísica, Astrobiologia e Climatologia). Participou do curso (EAD) de Astrofísica, concluído em 2020, pela Universidade Federal de Santa Catarina (UFSC).
>Autor de cinco livros, que estão sendo vendidos nas livrarias Amazon, Book Mundo e outras.
Acesse abaxo, os links das Livrarias>
https://www.amazon.com/author/heliormc57
https://publish.bookmundo.pt/site/userwebsite/index/id/helio_ricardo_moraes_cabral/allbooks
e-mail: heliocabral@coseno.com.br

Nenhum comentário:
Postar um comentário